Chapter 4 Polar form
There is another way of representing complex numbers, known as . Instead of representing a number in the complex plane as a distance along two axes, polar form represents it using the straight line distance from the origin, denoted \(r\), or \(|z|\) (for a complex number \(z\)) and a rotation by some angle \(\theta\), counter-clockwise starting at the \(x\)-axis.
This box summarises the different ways to write polar form. How to get the modulus and Argument are described in the rest of this section.
Polar Form:
\[z = | z | (\cos \theta + i\sin\theta) \text{ or }z = r (\cos \theta + i\sin \theta)\]
where, \(| z | = r\) is the modulus of \(z\) and \(\theta = \text{Arg}(z)\) is the argument of \(z\).
We have already discussed how to obtain \(|z|\), the straight line distance between the complex number and the origin, from a complex number in rectangular form: \(|z| = \sqrt{a^2 + b^2}\). We can find \(\theta\) using basic trigonometry (more details in next section).
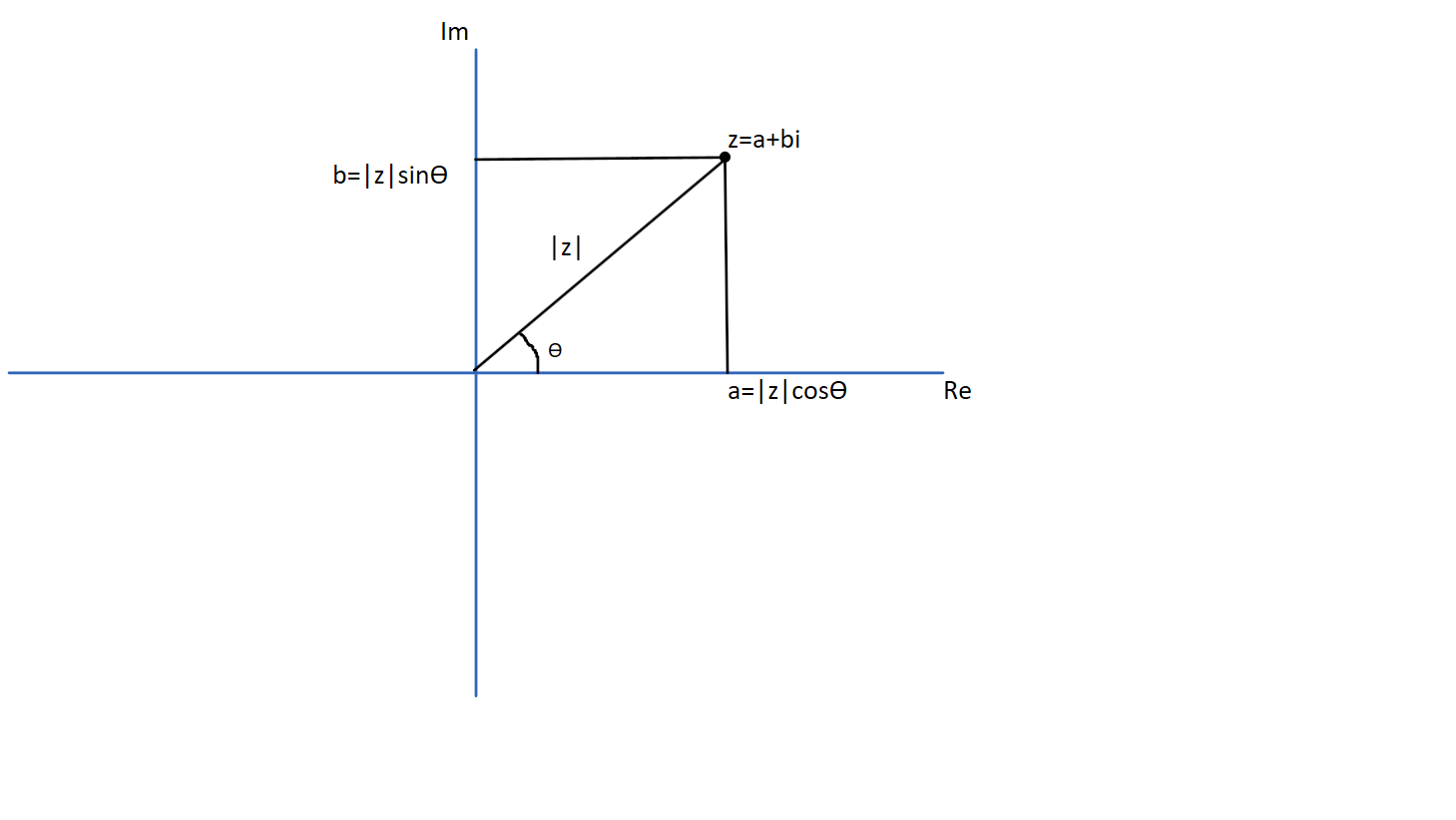
Argand diagram with components shown.
From the figure above, simple trigonometry can be applied to find expressions for the real, \(a\), and imaginary, \(b\), parts of the complex number - this allows us to convert from one form to the other! i.e.
Thus we get the final formula for the polar form of complex numbers,
which is \[z = |z| (\cos \theta + i \sin \theta)\]
: For \(\theta\), a principal value from the interval \((- \pi, \pi]\) is chosen, since \(\theta\) and \(\theta + 2 k \pi\) for any
integer \(k\) yield the same output when plugged into \(\sin\) or \(cos\)
4.1 Converting between forms
To convert a number \(z = a + bi\) from rectangular form to polar form, we must first find \(|z|\) and \(\theta\). Recall that \(|z|\) is the modulus of the complex number, given by \(\sqrt{a^2 + b^2}\).
4.1.1 Finding \(\theta\)
If you remember your definitions of trigonometric functions, you’ll find that \(\tan \theta\) is given by taking the opposite side and dividing by the adjacent side (soh cah toa). In the shown in the figure above, we get: \[\tan \theta = \frac{b}{a}\] and therefore \[\theta = \tan^{- 1} (\frac{b}{a}) .\] However, it is not so simple if the complex number falls into one of the other quadrants of the complex plane (but it still uses simple trig).
The following figure shows the quadrants:
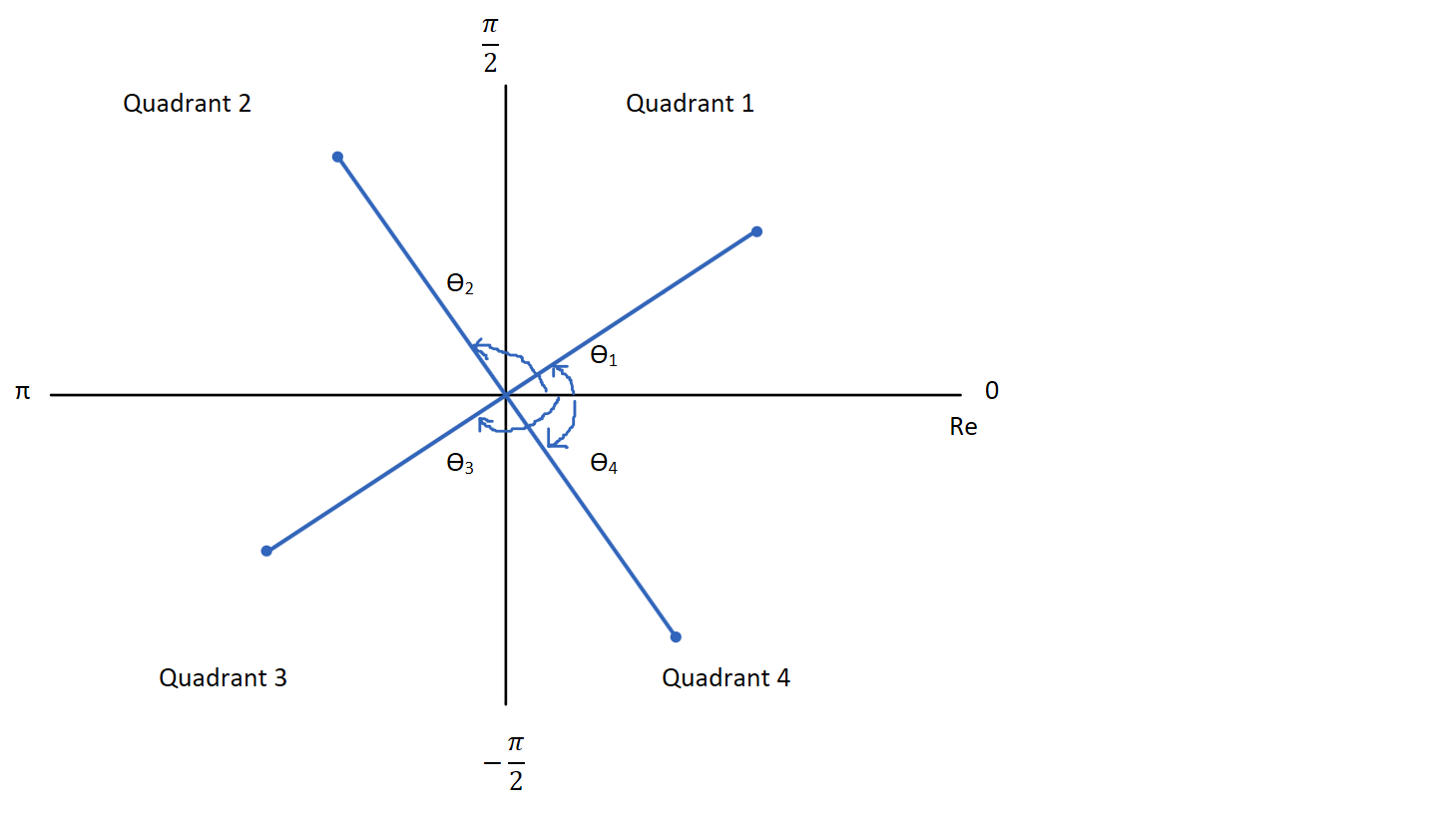
Complex numbers in each of the four quadrants with their respective arguments.
By convention the principle argument for a complex number takes the values \(- \pi\) to \(\pi\), i.e. \(\theta \in (- \pi, \pi]\). This means the top half of the complex plane (Quadrant 1 and 2) have a positive argument \(\theta_{1, 2} \in [0, \pi]\) and the bottom half of the complex plane (Quadrant 3 and 4) have a negative argument \(\theta_{3, 4} \in (- \pi, 0)\).
| Quadrant | Sign of \(a\), \(b\) | Formula for \(\theta\) | Range of \(\theta\) |
|---|---|---|---|
| 1 | \(a > 0\), \(b > 0\) | \(\theta = \tan^{- 1} \left( \frac{b}{a}\right)\) | \(\theta \in (0, \frac{\pi}{2})\) |
| 2 | \(a < 0\), \(b > 0\) | \(\theta =\pi-\tan^{-1}\left(\left|\frac{b}{a}\right| \right)\) | \(\theta \in (\frac{\pi}{2}, \pi)\) |
| 3 | \(a < 0\), \(b < 0\) | \(\theta = - \left( \pi - \tan^{- 1} \left( \left|\frac{b}{a} \right| \right) \right)\) | \(\theta \in (- \pi, - \frac{\pi}{2})\) |
| 4 | \(a > 0\), \(b > 0\) | \(\theta = - \tan^{- 1} \left( \left| \frac{b}{a}\right| \right)\) | \(\theta \in (0, - \frac{\pi}{2})\) |
The only case not covered in the table are when the complex number lies directly on the axes. Then the argument takes the values \(\theta = 0\), \(\theta = \frac{\pi}{2}\), \(\theta = \pi\), \(\theta = \frac{\pi}{2}\) for the positive real numbers, positive imaginary numbers, negative real numbers and negative imaginary numbers respectively.
To convert a complex number from polar form to rectangular form we just need to multiply the polar form out (everything becomes pretty clear then). \[z = |z| (\cos \theta + i \sin \theta) = r \cos \theta + ri \sin \theta = a + bi\] From this, it’s clear to see that \[a = r \cos \theta\] and \[b = r \sin \theta .\]