Chapter 5 De Moivre, Euler, roots

5.1 De Moivre’s Formula

De Moivre’s Formula is an important result, since it connects complex numbers with trigonometric functions. It has a close connection to Euler’s formula, can be used to find roots of complex numbers and to derive certain trigonometric identities. It states that for a real number \(\theta\) and integer \(n\), it holds that

De Moivre’s Theorem: \[(\cos \theta + i\sin \theta)^n = \cos (n \theta) + i \sin (n\theta)\]

This can be proven using induction.
We can use De Moivre’s formula to find certain trigonometric identities, such as the formulae for \(\cos (nx)\) and \(\sin (nx)\). For example, if \(n = 2\), we have

\((\cos x + i \sin x)^2 = \cos (2 x) + i \sin (2 x)\)

We can expand the right hand side using the binomial theorem to get:

\(\cos^2 x + 2 i \sin x \cos x - \sin^2 x = \cos (2 x) + i \sin (2 x)\)

We gather the real and imaginary components together to get:

\((\cos^2 x - \sin^2 x) + i (2 \sin x \cos x) = \cos (2 x) + i \sin (2 x)\)
\(\cos (2 x) = \cos^2 x - \sin^2 x\) and \(\sin (2 x) = 2 \sin x \cos x\)
which you might remember are the exact formulae for \(\cos (2 x)\) and \(\sin (2 x)\).

5.2 Euler’s Formula

Closely related to De Moivre’s formula is Euler’s formula. It connects trigonometry, complex numbers, and exponents as well. It states that for any real number \(\theta\) it holds that

\(e^{i \theta} = \cos \theta + i \sin \theta\)

For the value \(\theta = \pi\), it yields so called Euler’s identity:

\(e^{i \pi} + 1 = 0\)

Given the connection between Euler’s and De Moivre’s formula, we can represent complex numbers as an exponent. For a complex number with polar form \(r (\cos \theta + i \sin \theta)\), it’s exponent form is \(re^{i \theta}\).

We now have three ways to write a complex number:

\(z = a + bi\) \(z= r (\cos \theta + i\sin \theta)\) \(z = re^{i\theta}\)

5.3 Roots of complex numbers

Like with real numbers, you can always find \(n\)-th roots of complex numbers. In other words, for a complex number \(z\) you can find complex numbers \(x\) such that \(x^n = z\). We can rewrite this as \(x^n - z = 0\) and thus get a polynomial in \(x\). Using the fundamental theorem of algebra we can prove it has exactly \(n\) distinct solutions for the value of \(x\). The \(n\)-th roots of a complex number are found at equally spaced angles around the complex plane and have the same modulus - they create an n-gon shape!

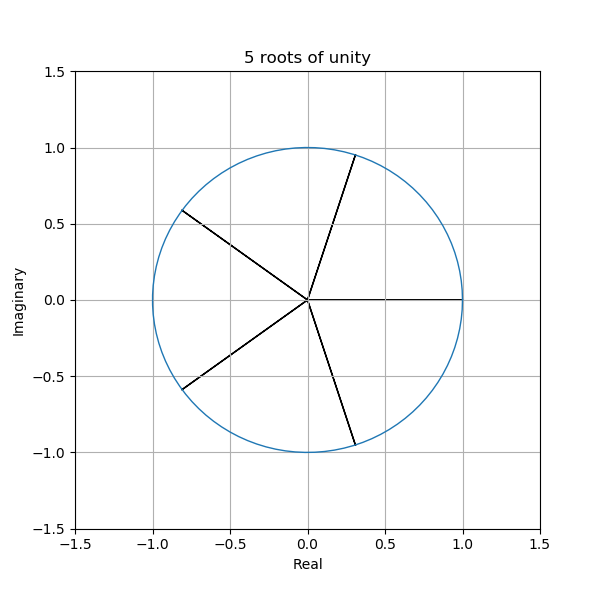
The five roots of unity shown on the unit circle.

Notice the axis of symmetry through the real axis. This is a consequence of the fact that if a complex number \(z\) is a root of a polynomial, then so is \(\bar{z}\).

5.4 Finding the roots

How do we go about finding the roots of a complex number? This is most easily done in exponential (or polar) form, i.e. write the complex number as \(z = re^{i \theta}\).

Notice that any point on the plane remains the same if we add a full revolution of \(2 \pi\), or two full revolutions \(4 \pi\) (or infact any number of revolutions) so let’s write: \[z = re^{i (\theta + 2 k \pi)},\] where \(k \in \mathbb{Z}\) (any integer).

Now if we want to find the n-th root we can simply use rules of indices: \[\begin{aligned} \sqrt[n]{z} = z^{\frac{1}{n}} & = (re^{i (\theta + 2 k \pi)})^{\frac{1}{n}}\\ & = r^{\frac{1}{n}} \exp \left( \frac{i (\theta + 2 k \pi)}{n} \right)\end{aligned}\] Now to find each root take \(k = 0\), \(k = 1\),..., \(k = n - 1\)!

Here is an example to illustrate this in action. Find the 4th roots of \(z = 1 - i\). We first rewrite this in exponential form: \[\begin{aligned} r & = |z| = \sqrt{1^2 + (- 1)^2} = \sqrt{2}\\ \theta & = - \tan^{- 1} \left( \left| \frac{- 1}{1} \right| \right) = - \frac{\pi}{4} \quad \text{since we are in quadrant 4}\\ & \Rightarrow z = \sqrt{2} e^{i (- \frac{\pi}{4} + 2 k \pi)}\end{aligned}\]

We can then easily find the 4th roots:

\[\begin{aligned} z^{\frac{1}{4}} & = \left( \sqrt{2} e^{i (- \frac{\pi}{4} + 2 k \pi)} \right)^{\frac{1}{4}}\\ & = 2^{\frac{1}{8}} \exp \left( i \left( - \frac{\pi}{16} + \frac{k \pi}{2} \right) \right)\end{aligned}\] The first root, call it \(\omega_0\), is found when \(k = 0\): \[\omega_0 = 2^{\frac{1}{8}} \exp \left( i \left( - \frac{\pi}{16} + \frac{0 \pi}{2} \right) \right) = 2^{\frac{1}{8}} e^{\frac{- i \pi}{16}}\] Second root, when \(k = 1\): \[\omega_1 = 2^{\frac{1}{8}} \exp \left( i \left( - \frac{\pi}{16} + \frac{\pi}{2} \right) \right) = 2^{\frac{1}{8}} e^{\frac{i 7 \pi}{16}}\] Third root, when \(k = 2\): \[\omega_2 = 2^{\frac{1}{8}} \exp \left( i \left( - \frac{\pi}{16} + \frac{2 \pi}{2} \right) \right) = 2^{\frac{1}{8}} e^{\frac{i 15 \pi}{16}}\] Fourth root, when \(k = 3\): \[\omega_3 = 2^{\frac{1}{8}} \exp \left( i \left( - \frac{\pi}{16} + \frac{3 \pi}{2} \right) \right) = 2^{\frac{1}{8}} e^{\frac{i 23 \pi}{16}} = 2^{\frac{1}{8}} e^{\frac{- i 9 \pi}{16}}\] where the final step converts the angle into the principle argument by adjusting it to lie in the range \((- \pi, \pi]\).